Speeding up text generation by LLM
On a high level, a Large Language Model is a function, which takes an input text + some “weights” and outputs a list of probabilities for all possible next words. When predicting the next word the computer’s processing unit (e.g. CPU) needs to have the text + all weights, but the CPU cannot store all the weights, so they need to be shipped to the CPU from memory and hard drive continuously. However, there is at least at the time of writing a practical fact - the CPU does its number crunching faster for a chunk of weights than than next set of weights arrives from memory. If CPU is a knife and text + weights is a salami, then the knife quickly slices up the salami and idles until the next part of salami (aka weights) arrives. Can this wasted idling be avoided to achieve faster performance on running the LLMs decoding process?
The answer is yes. We will in effect follow the ideas as outlined in “Accelerating Large Language Model Decoding with Speculative Sampling” by C. Chen et al 2023. Here we will also approach by a more visual and intuitive path to the proof of the “Modified Rejection Sampling” scheme, which is a fun sampling puzzle.
The upcoming discussion assumes a basic understanding of the functioning of LLMs.
The idea - draft and verify
Here is a handy observation - we could avoid idling the CPU if we processed multiple text inputs at the same time. That would be nice, but LLMs generate a sequence of inputs. Ie. the next input depends on the output of the previous output, so what sort of set batch of “texts” should we be processing at the same time?
The idea is to use a quicker LLM model (eg. a smaller LLM model with fewer weights) to generate a draft sequence - then use the big model to “verify” the outputs of the draft model. If the big model deems a word in the draft sequence is not good enough, it discards the rest of the drafted sequence and continues the generation from the latest location.
Clearly, the hope here is that the draft LLM model is “good enough” for significant parts of the text. But what would be the intuition for such a guess? Roughly speaking - because some parts of sentences contain more information and some less. For example, the top hundred english language words will cover about half of the words in all texts. However, all the interesting and valueable words are actually the other ones. Here are a few top English language words - “a, about, all, also, and …”. If we consider the sentence “They decided to _ but then changed their minds and _” - most of the excitement is in the missing parts giving all the information what the story is about.
There is a practical question to this, however - doing extra sampling by the draft model takes extra time, so is this extra time worth spending given discarding? There is a tradeoff here. Turns out that as practical observation yes, it is (see C. Chen 2023).
The sampling
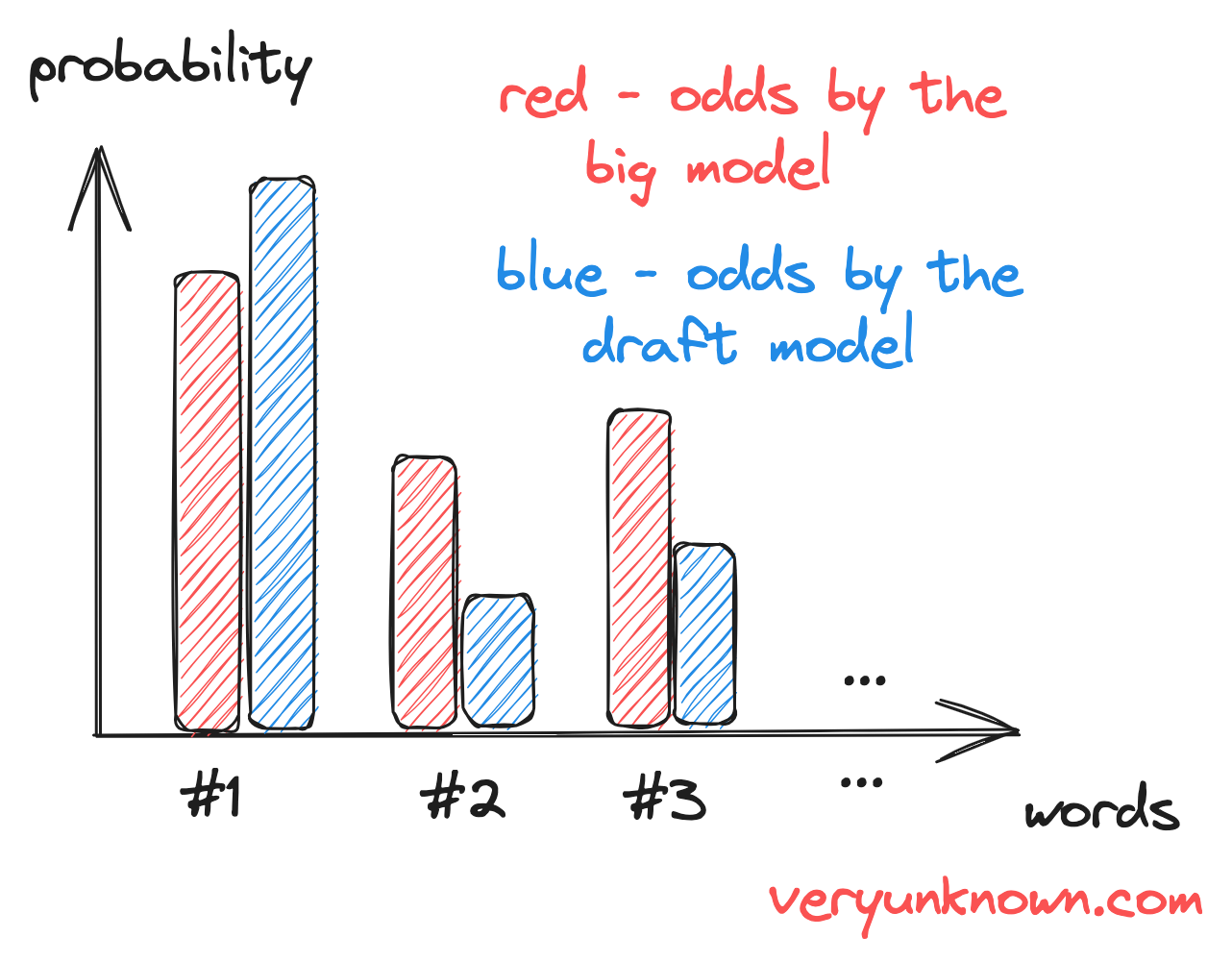
Fig 1. Probabilities for each word for the large and the draft LLMs
In the last section, we noted that the quick model “drafts”. The drafting concept is straightforward - use the quick model first to decode a few words ahead (and keep the full list of probabilities for each word). Then use the big model to calculate for each input the output word probabilities - which can be done for a batch of inputs. So far so good, however, how are we to use the big model to “verify” outputs? This is a probabilistic model - outputs are not just “right” or “wrong”.
Let us consider Figure 1. It shows probabilities for an input text for each possible next word as given by the draft model and by the big model. As expected, probabilities will not match between the draft model and the big model, but what we want is to have an algorithm to make them equal. We will base our plan around the following - note, how the draft model for words #2 and #3 underestimate probabilities. If the draft model underestimates some probabilities, then it must be overestimating them for other words - e.g. word “#1”. Ie. some words have “stolen” some probability from other words, and we should restore the balance by returning them back.
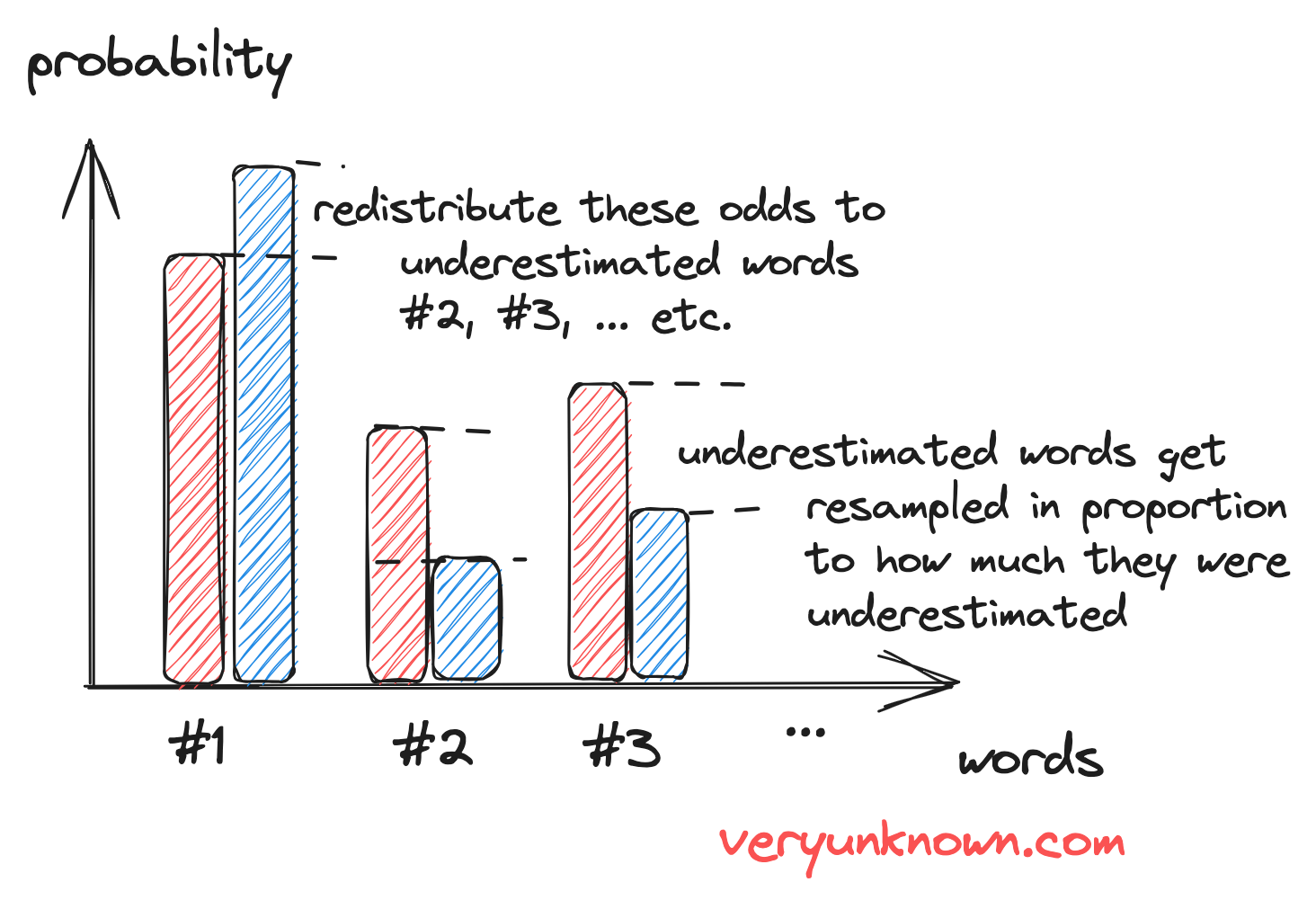
Fig 2. Redistribution of the excess probability of draft LLM
To restore the balance, the drafted words with underestimated odds by the draft model will always get accepted by our algorithm. However, if the odds are overestimated, then we want to return the “extra probability” back (and only the “extra”). Let us consider Figure 2. For the word #1 we still want to keep it sometimes - the same amount as the large model’s odds. So we will roll a die, and keep the word with odds “probability of red” : “probability of blue” for word #1 (“odds” as in “betting odds”, not “probability”), otherwise we reject the drafted word, and sample a new one from all the words which were underestimated - each in proportion to how much they were underestimated with respect to large language’s model’s probabilities.
If we did keep the drafted word, we proceed to the next drafted word, otherwise, we start the drafting and verification cycle again for the next span of words.
Summary of algorithm
Let us summarise the above discussion
Sample sequence of K words by the quick model as a draft (and keep the full output odds \(p\) for each input). Calculate for the K drafted words in batch the probabilities as given by large LLM (we will call them \(q\)). For each word \(w_{draft}\) of the K drafted word we then do the following in sequence. If \( p(w_{draft}) < q(w_{draft}) \) then accept the drafted word and move on to checking the next one. Otherwise, we keep the drafted word by sampling with odds \( q(w_{draft}):p(w_{draft}) \) (aka generate random \(x\) in range 0 to 1 and keep the drafted word \(w_{draft}\) if \( x < q(w_{draft})/p(w_{draft}) \)). However, if the drafted word was discarded, we sample a word from all the underestimated words with odds in proportion to how much they were underestimated \( (q(w_2)-p(w_2)) : (q(w_3)-p(w_3)) : \dotsc \) and stop looping over the draft K words. If we happened to cycle through all K draft words successfully, generate one extra word by big model, and return start the process all over.