Language and thought
We will be be talking about a language, a notation originated by Roger Penrose - the 2020 Nobel Prize winner in Physics. Language has an impact on how we think and perceive things. For example, there is a language in Australia that does not have relative directions like “left” or “right”, but always points in specific directions like “east” or “west”. Or how languages have words for concepts that don’t have direct equivalents in other ones. For example, “schadenfreude” in English is taken from German. Having a word immediately helps to formulate a concept and e.g. notice it. Such considerations also apply to mathematical notation. For example, one can visualize some proofs with pictures like Euclid’s elements, and at the same time, the same proofs could be expressed by algebraic manipulations. Same thoughts and ideas, different language. Here we will be talking about vector calculus and a different notation for it than commonly encountered - a first introduction to Penrose graphical notation.
Knowledge of vector calculus is a prerequisite in what follows.
Why bother with a new notation for vector calculus? One already needs to deal with two of them - expressions in component form, and expressions in vector form. First reason - for fun! Its a graphical notation, and humans are very visual creatures, so having notation that looks like pictures is pleasing. This has practical benefits - it’s easier to notice things about pictures, than abstract symbols, as well it’s easier to remember pictures than algebraic identities. This lends to practicality. But it also helps to move towards better insights. Vector calculus is great - but it has been made to fit 3-dimensional Euclidean space, ie. what we call “normal space”. But since Special and General relativity it has been known that we live in 4-dimensional “space-time” (eg. see “Inventing special relativity”). How does “vector calculus” generalize to 4 dimensions? And even more, how would it work in non-Euclidean space? We will not explore this here, but Penrose graphical notation is very nice as we move towards such questions and physical problems.
But for now, we will stay in our comfortable 3-dimensional space with time as a separate thing, stay in the Cartesian coordinate system, and have the first introduction to the notation. We will elide quite a few details to keep it first introduction friendly.
The basics
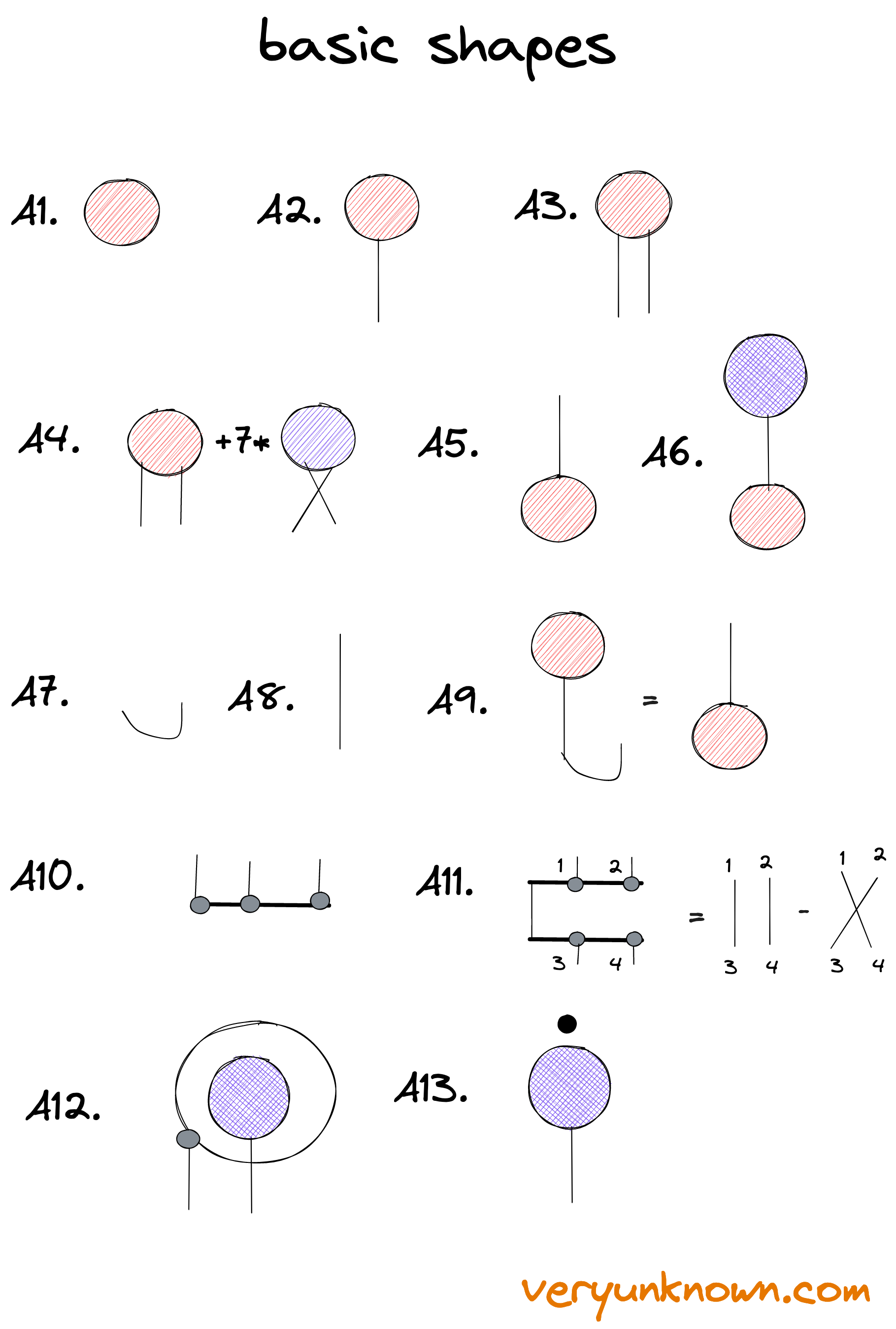
Fig 1. Basic shapes
Lets see all the basic visualizations for basic things in Figure 1. Note, we will assume working in 3 dimensional space and in Cartesian coordinate system
- A simple number \(x\) is just some shape, without any “legs”
- A vector has multiple components, so there must be index to enumerate them, and the leg represents the index. That is picture represents \(v_i\)
- This basically represents an entity with two indexes [1]. That is picture represents \(v_{ij}\)
- We can do normal operations like addition, multiplication etc., ie. \(a_{ij} + 7b_{ji}\)
- A leg can point upwards. That is picture represents \(v^i\). We think of such things alike a vector, and will call them “co-vector”
- Joining upwards and downwards legs represent “inner product” for the index - ie. multiply pairwise elements and add them up. Ie. \(\sum a^ib_i = a^0b_0+ a^1b_1 + a^2b_2 \) . Ie we can join legs pointing in opposite directions and get back a regular single number, ie. notice, how there are no “legs” - we have object like in point (1)
- The curve represents a Kroncker delta with two lower indexes - \(\delta_{ij}\). Ie. for \(i=j\) value is 1, otherwise 0 [2]. We haven’t drawn it but there is also inverted version - \(\delta^{ij}\).
- The line represents a Kroncker delta with one index upwards, and one downwards - \(\delta_{i}^{j}\)
- This is not new, but combines pictures (2)/(6)/(7). We can use (7) to flip direction of legs. We in effect turned (2) into (5). We could also turn (5) into (2) with the inverted version of curve. In effect, we can flip legs up and down, because of (7). We will mostly elide drawing (7) when changing direction of a leg.
- Levi-Civita symbol \(\epsilon^{ijk}\). If any pair of indexes are the same, then it is 0, and \(\epsilon^{123}\) = 1, but each swapping of indexes swaps the sign, e.g. \(\epsilon^{213}\) = -1 as we swapped indexes once - the 1 and 2.
- This is identity of what happens if two (10) shapes are joined with (6). We will not prove it here, but follows straightforwardly from definitions
- A larger circle around original shape is space derivative. It creates new object of type (3). Ie. it represents \(\partial_jv_i\)
- We treat time uniquely, and use Newton’s notation for time derivative - a dot over the value. The picture represents \(\partial_tv_i \equiv \dot{v_i}\)
Gradient operator
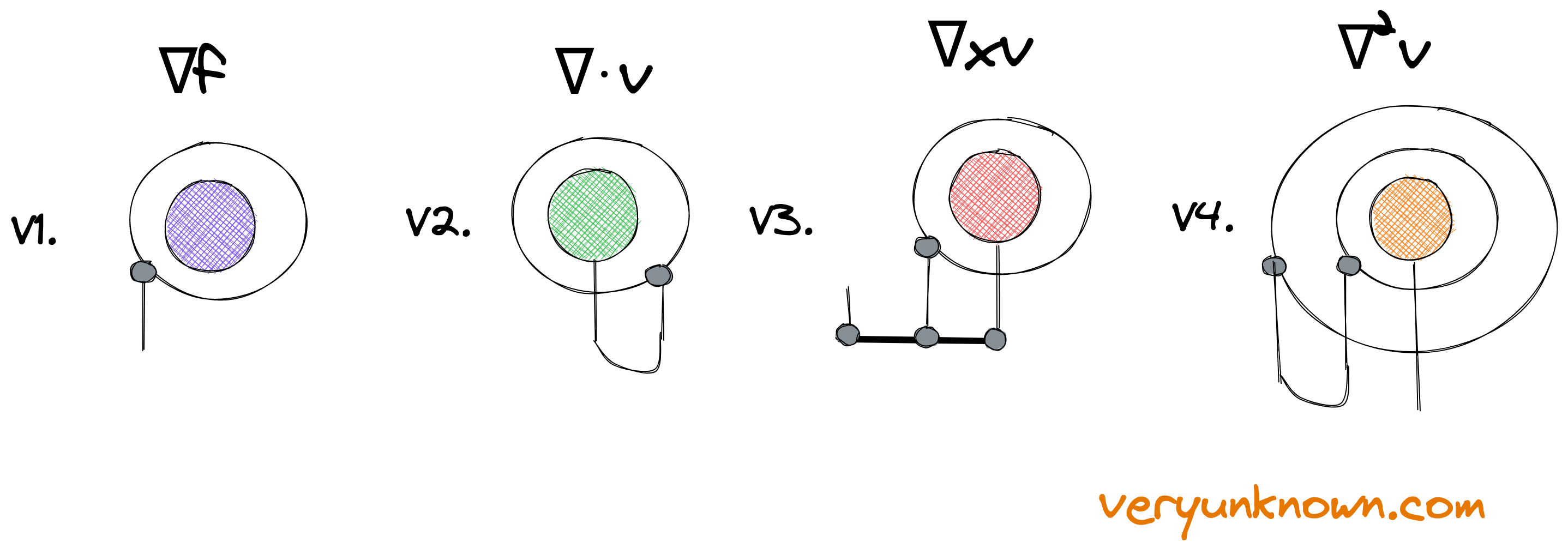
Fig 2. Operators involving gradient
We have in the last section defined quite a lot of things. Now, let us apply them in expressing the gradient operators from standard vector calculus in our new notation - see Figure 2.
Maxwells equations
Let us apply our new notation to physics! First we will write down Maxwell’s equations. Then to exercise muscles using the notation practically - we will apply the notation to an iconic derivation. We will derive wave equation from Maxwell’s equations!
Fig 3. Maxwell’s equations and deriving wave equation from Maxwell’s equations
A peep forwards
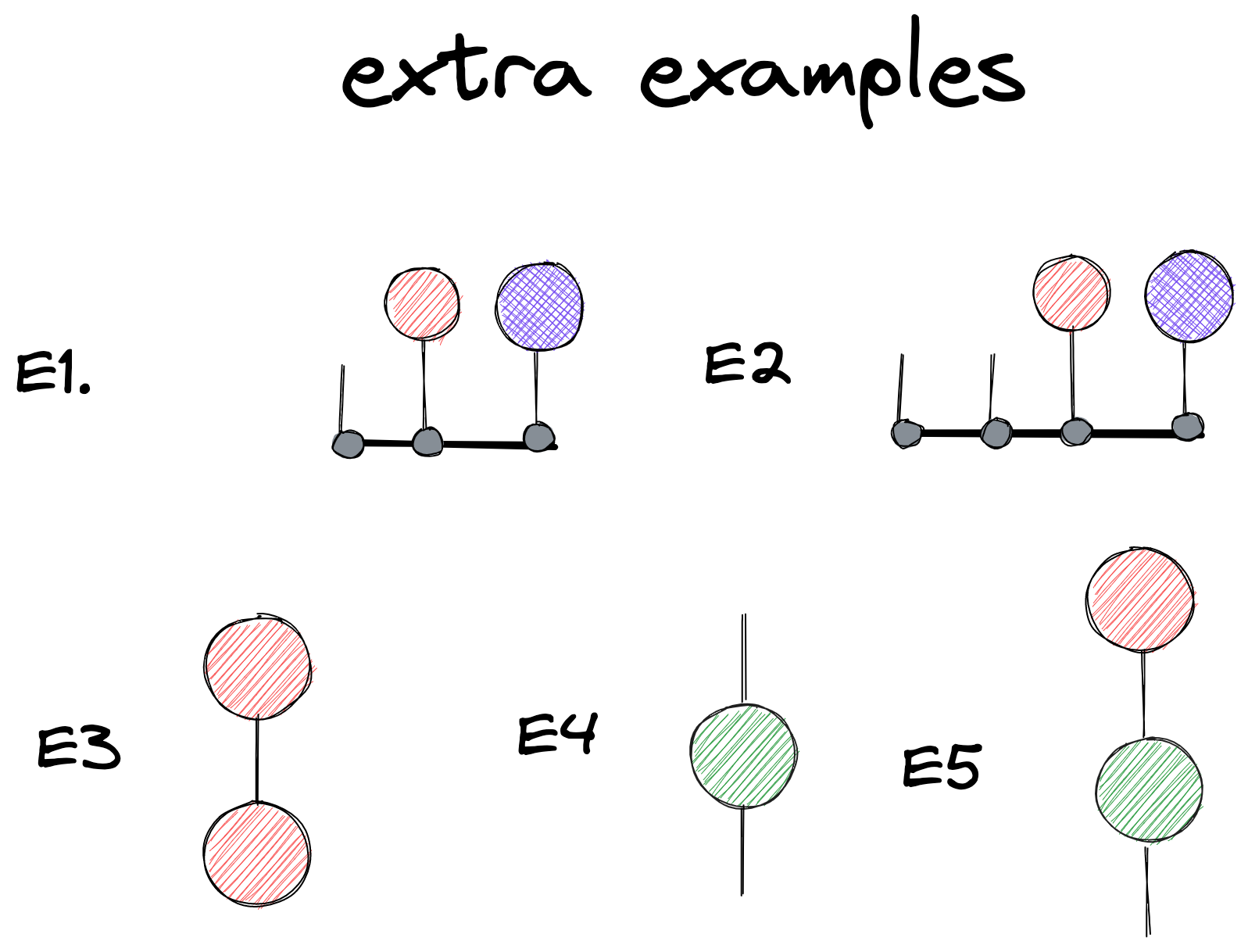
Fig 4. Extra shapes
We have introduced and applied the Penrose graphical notation to something useful, which is great! But thus far we have mostly only repeated what we could already do - can we start seeing some illumination ahead beyond handy mechanical machinery?
For example, let us consider “cross product” in this notation in E1 in Figure 4, and remind ourselves of the geometric meaning of cross product - it gives direction of plane (and numeric value of its area), and it is visualized as a vector. It is obviously visible that what is left is one free leg in E1, like A2 in Figure 1, which matches well with the geometric understanding of “cross product” as vectors are one-legged objects. But what happens if we try to generalize to 4D - it is not an accident that the Levi-Civita symbol in 3D had 3 legs. In 4D we would have 4 legs. But in 4D the 4 legs minus 2 legs leave 2 legs free (see E2), not one. This is not a vector anymore. What does this mean geometrically? A plane can be defined by its two edges, and in 3D there is only one unique direction perpendicular to the plane. But in 4D - there is more than one perpendicular direction to a plane! The notion of regular cross-product does not transfer to 4D. Graphical notation makes that easy to see.
Or here is another example of what notation highlights - our ability to flip legs up and down depended on the existence of a 2 legged thing A7 in Figure 1. But what is the thing A7 more precisely [2]? Having it allows us to assign a number to any vector - E3 in Figure 4. What is this number? If we follow the definitions in 3D Cartesian coordinate system the E3 equals \(a^0a_0+ a^1a_1 + a^2a_2 = a^2_0+ a^2_1 + a^2_2\) . This looks like the Pythagorean theorem - it assigns length for a vector! Ie. having A7 means we have the notion of “length” in our math. Can we have A7 not defined? We can indeed - for example, if we talk about the math of e.g. rubbery objects [3]! In such a case, we cannot just flip the legs up and down freely as we have done above.
Is the notation only applicable to “vector calculus”? Not at all. For example, we can apply this to linear algebra - we could draw a matrix as an object with one leg up, and one leg down (see E4 in Figure 4), and then matrix multiplication with a vector would be represented as E5 in Figure 4. Note, how the result is a one-legged object, as expected - a vector.
This has been a very quick introduction to Penrose graphical notation. It’s a handy and helpful notation, and most importantly - it is rather fun.
[1] Two legs mean this is rank 2 tensor
[2] It is a metric tensor, but we are working in 3 dimensional Cartesian coordinate system
[3] In other words, topology